Teknik Uji-T Sampel Bebas (Independent Sample T-Test) 2016

1.        Pengertian Uji-T sampel bebas

Suatu penelitian yang bertujuan untuk mengetahui perbedaan (hasil belajar, kinerja karyawan, pendapatan perusahaan, kecepatan, dan lain) antara dua kelompok, yaitukelompok control dan kelompok eksperimen tidak akan pernah lepas dari yang namanya statistic. Statisticyang digunakan untuk menganalisis perbedaan diantara dua kelompoktersebut adalah UjiT sampel bebas. Ujisampel bebas atau yang sering dikenal dengan istilah Independent Sample T Test adalah teknik analisis data yang digunakan untuk mengujibeda mean2 sampel yang independen yang datanya interval/rasio.

Sebelum menggunakan teknik analisis UjiT sampel bebas, peneliti terlebih dahulu harus menguji normalitas distribusi dan homogenitas varians dari data tersebut. Jika datatersebut berdistribusi normal dan memiliki homogenitas yang sama (homoskedastisitas) maka dapat digunakan teknik analisis UjiT sampel bebas. Dan sebaliknya jika data berdistribusitidak normal atau tidak homogen (heterokedastisitas) maka tidak dapat menggunakan Uji-T, sebagai penggantinya adalah dengan menggunakan mann-withney U-tes, K-S, Median tes, danlain-lain.

2.        Analisis Uji-T sampel bebas

Ada sebuah kasus seperti berikut:  seorang guru berhipotesis  “ada perbedaan signifikasis hasil belajar siswa yang mengikuti pembelajaran langsung dan pembalajarankooperatif”. Untuk itu ia melakukan eksperimen untuk mengujicobakan model pembelajaran kelas X1 diterapkan model pembelajaran langsung dan kelas X2 diterapkan modelpembelajaran kooperatif. Data hasil eksperimen ditunjukan pada tabel 1 di bawah ini. Dengan taraf kesalahan 5% apakah hipotesis guru dapat diterima? (dengan catatan databerdistribusi normal dan homogen)

Tabel 1

No.	HB MPK	HB MPL
1	63	65
2	75	75
3	60	75
4	76	85
5	63	85
6	78	80
7	88	85
8	73	70
9	58	85
10	68	85
11	73	90
12	75	70
13	68	85
14	85	75
15	68	75

a.          Hipotesis

a)        H₀ : HB MPL = HB MPK

b)       H₁ : HB MPL ≠ HB MPK

b.        Mengoperasikan SPSS

a)        Buka aplikasi SPSSyang antum miliki seperti pada uji normalitas dan homogenitas variansi, sehingga muncul tampilan seperti pada gambar 1 di bawah ini.

Gambar 1. Tampilan awal SPSS

b)        Klik variableview yang ada di pojok kiri bawah dari spss seperti pada uji normalitas, sehingga akan muncul seperti gambar 2 di bawah ini.

Gambar 2. Variable view yang belum diisi

c)         Buatlah lapak dengan ketentuan seperti di bawah ini:

ü  Name: Isi dengan nama variable anda (terserah mau diberi nama apa saja biasanya dalam bentuk singkatan), dalam hal ini saya mengisinya dengan 

       kata “NHB” untuk baris1 dan “Klp” untuk baris 2.   

ü  Type: Pilih Numeric

ü  Width: Isi dengan angka 8

ü  Decimal: Isi dengan angka 2 untuk baris 1(terserah user) dan isi dengan angka 0 untuk baris 2 (wajib)

ü  Label: Isi dengan kepanjangan dari name di atas, dalam hal ini saya              mengisinya dengan  “Nilai Hasil Belajar” untuk baris 1 dan “Kelompok” untuk baris 2.

ü  Value: pilih none untuk baris 1 sementara untuk baris 2 pilih dengan ketentuan sebagai berikut:

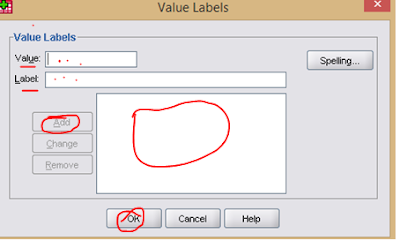
1.        Klik pada kolom value, sehingga muncul kotak dialog seperti di bawah ini.

Gambar 3. Kotak dialog value

2. Bagian value isi angka 1 dan pada bagian label-nya isi dengan MPK kemudian klik add (persis di bawahnya label).

3. Bagian value isi angka 2 dan pada bagian label-nya isi dengan MPL kemudian klik add (persis di bawahnya label).

4.        Kemudian klik ok

ü  Missing: Pilih none

ü  Columns: Isi dengan angka 8

ü  Align: Pilih right (terserah user)

ü  Measure: Pilih scale

Gambar 4 Tampilan varible view yang sudah di isi

d)       Kalau sudah selesai klik data view (sebelahnya variable view)

e) Masukkan data nilai MPK dan MPL ke dalam kolom “NHB” yang ada di spss dengan di ketik atau copas dan isikan angka “1” sampai baris ke 15, serta isikan angka “2” daribaris 16 – 30.

Gambar 5. Tampilan data view yang sudah di isi

f)          Klik menu analyze- pilih compare means – pilih Independent-sample T test

Gambar 6. Langkah-langkah pengoperasian

g)        Akan muncul kotak dialog seperti di bawah ini

Gambar 7. Kotak dialog independent sample Ttest

h)        Pindahkan (1). variable “Nilai Hasil Belajar (NHB)” ke kolom tes variable dengan cara klik “Nilai Hasil Belajar (NHB)” kemudian klik tanda panah yang mengarah ke tesvariable (è). (2). Variable “Kelompok (Klp)” ke kolom “grouping varibel” dengan cara klik “Kelompok (Klp)”kemudian klik tanda panah yang mengarah ke grouping varibel(è).

Gambar 8. Kotak dialog independent sample T tes

i)          Klik define groups- pada kotak dialog define groups pilih use specified values-group 1 isi dengan “1” dan group 2 isi dengan “2”. Kemudian klik continue.

Gambar 9. Kotak dialog define group

j) Klik option – pada kotak dialog independent sampel T-tes: option, terdapat convidence interval isi dengan “95”. Klik continue.

Gambar 10. Kotak dialog independen

k)        Klik ok

l)          Output

Gambar 11. Output

m)     Pengambilan keputusan

ü  Pertama kita harus menentukan homogenitas varians dengan cara melihat sig. pada kolom leven’s, apakah termasuk equal variances assumed atau equal variance not asseumed.(Baca: homogenitas varians)

ü  Untuk melihat signifikansi perbedaan hasil belajar (MPL dan MPK) adalah pada bagian sig. (2-tailed) dan yang sejajar dengan equal variances assumed atau equal variance notasseumed.

ü  Jika sig. lebih besar dari 0,05 maka terima H₀ (HB MPL = HB MPK)

ü  Jika sig. kurang dari 0,05 maka terima H₁ (HB MPL ≠ HB MPK)

3.        Kesimpulan

a.    Berdasarkan hasil hitung spss diperoleh nilai F 0,114 dengan signifikansi 0,738 dengan demikian dapat disimpulkan terima H₀  yang menyatakan variansi dari nilai siswa yangdiajar dengan model MPK dan MPL 
     memiliki variansi yang homogeny (sama) equal variances asseumed. 
     (baca: homogenitas varians )

b.   Berdasarkan hasil hitung spss diperoleh t -2,595 df 63 dan signifikansi 0,015. Karen sig. (2-tailed) < 0,05 dengan demikian maka disimpulkan terima H₁ yang berarti 
    bahwa skor rata-rata hasil belajar mapel listrik dengan metode MPK dan MPL 
     terdapat perbedaan yang signifikan.

Daftar Pustaka

Sudjana. 2005. Metoda Statistika. Bandung: Tarsito.

Ismed, Basuki dan Sudarmono. 2014. Pengujian Hipotesis (ppt 6 pengujian hipotesis). Surabaya

Hasan, Iqbal. 1999. Pokok-poko Materi Statistik . Jakarta: PT. Bumi Aksara

Hanafiah, Kemas Ali. 2010. Dasar-dasar Statistika : aneka bidang ilmu pertanian dan hayati. Jakarta:   Rajawali Pers

Hamang, Abdul. 2005. Metode Statistika. Yogyakarta: Graha Ilmu